C/C++实现双路快速排序算法原理
时间:2020-10-05 21:32:37 | 栏目:C代码 | 点击:次
本文实例为大家分享了C/C++实现双路快速排序算法的具体代码,供大家参考,具体内容如下
看了刘宇波的视频,讲双路快速排序的,原理讲的很直观,程序讲解也一看就懂。这里写一下自己的理解过程,也加深一下自己的理解。
首先说一下为什么需要双路排序,在有些带有许多重复数据的数组里,使用随机快速排序或者最简单的快速排序算法时,由于重复的数据会放在原来的索引位置不动,就回导致划分数组时划分的某一部分太长,起不到分段排序的效果,这样就导致算法退化成O(n^2)的复杂度。就像下图:
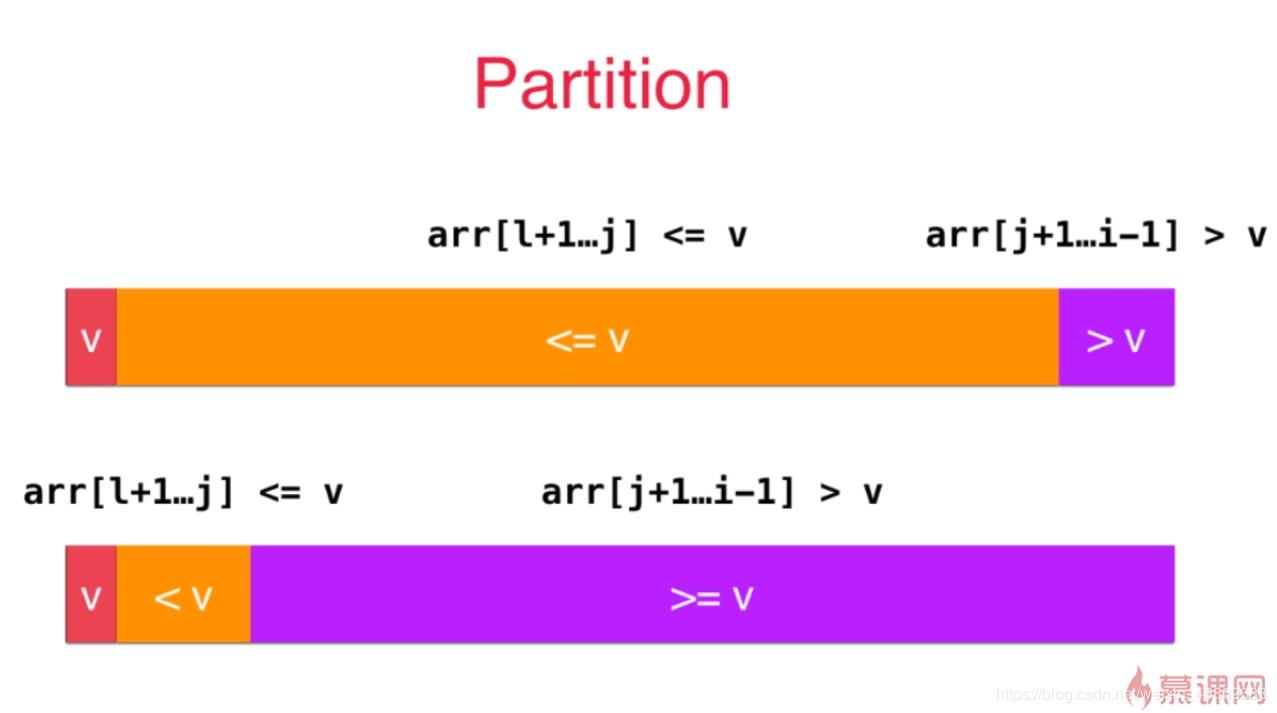
为了解决这个问题,双路快速排序采用的方法是对等于v的数也进行交换,原理如下所述:
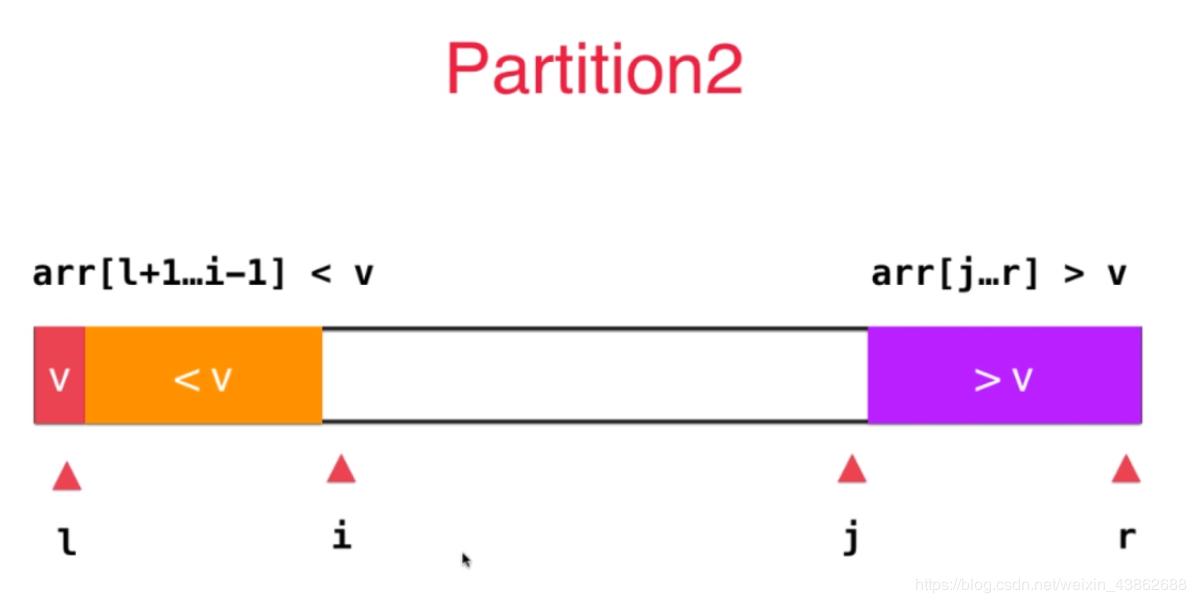
首先选择一个数作为标志,放在数组的最左侧,下标为l,在数组左边放小于v的数,右侧放大于v的数。
之后,先从l+1开始遍历数组,当数据小于v时,该数据属于左侧橙色部分,保持其位置不动,i++,继续向后遍历,当找到某个数大于或者等于(注意,这里等于很重要)v时,停止遍历。转而开始根据j来遍历数组,j不断减小,索引数组的数据,当索引到某个数小于或者等于v时,停止遍历。如下图所示:
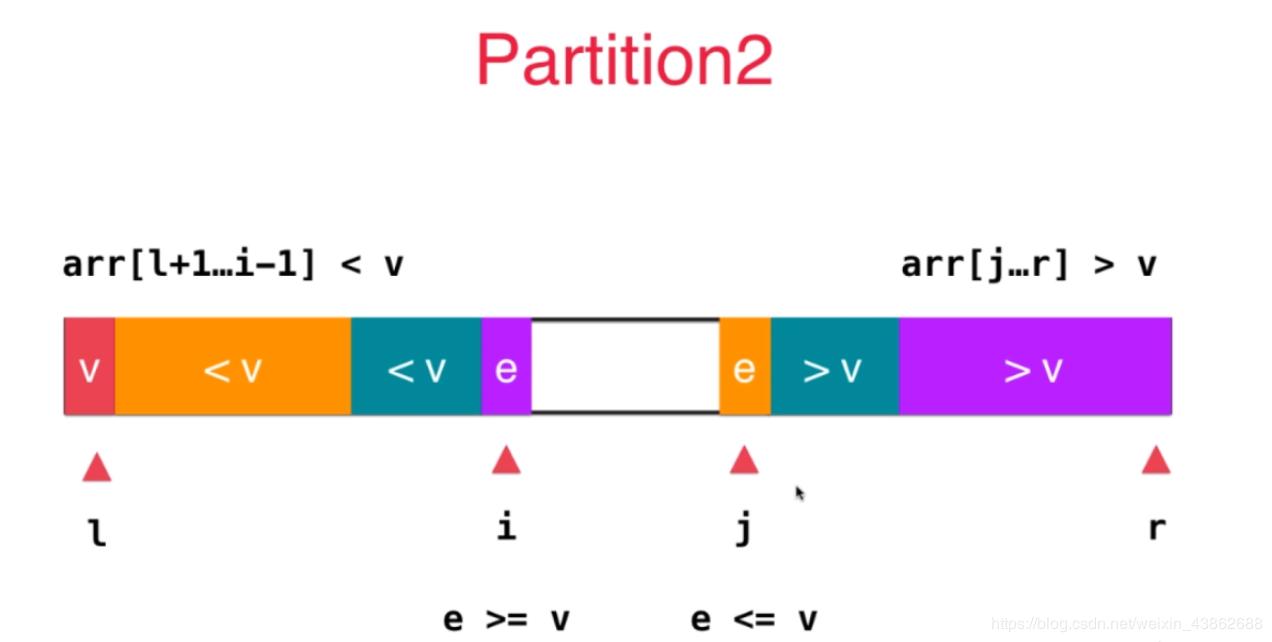
这时两个绿色的区域就是分别属于<v和>v的部分,而i,j所对应的索引数据要交换位置。
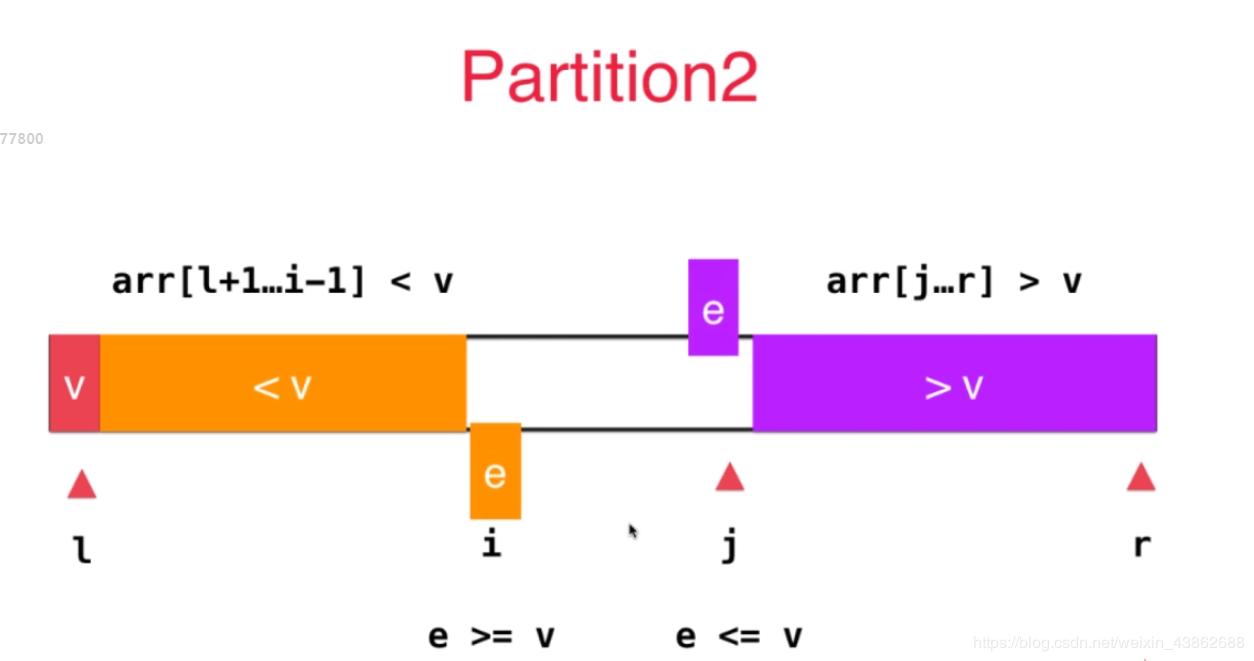
之后,将i,j分别向后向前移动一位,继续开始新的索引,直到i和j重合或者i>j位置,就完成了partition的过程。
下面贴出代码:
主函数 main.cpp
// QuickSort2.cpp : 双路快速排序,适用于解决有很多重复数据的数组。
//
#include "stdafx.h"
#include "E:/学习/C++/数据结构和算法/code/算法/排序算法/common/sortTestHelper.h"
#include "QuickSort.h"
#include "RadomQuickSort.h"
#include "QuickSort2.h"
using namespace std;
int main()
{
int n = 100000;
int *arr1 = SortTestHelper::generateRadomArray(n, 0, 50);
int *arr2 = SortTestHelper::generateRadomArray(n, 0, 50);
int *arr3 = SortTestHelper::generateRadomArray(n, 0,50);
SortTestHelper::sortTime("随机快速排序", RadomQuickSort, arr1, n);
SortTestHelper::sortTime("快速排序", QuickSort, arr2, n);
SortTestHelper::sortTime("双路快速排序", QuickSort2, arr3, n);
delete[] arr1;
delete[] arr2;
delete[] arr3;
return 0;
}
双路快速排序算法 QuickSort2.h
#ifndef QUICKSORT2_H
#define QUICKSORT2_H
#include <stdlib.h>
#include <iostream>
using namespace std;
template <typename T>
int __partition3(T *arr, int l, int r)
{
//此处结合随机快速排序的算法进行了优化,标记点在数组里随机选择
int RAND = (rand() % (r - l + 1) + l);
swap(arr[RAND], arr[l]);
int v = arr[l];
int i = l + 1;
int j = r;
while (true)
{
while (i <= r&&arr[i] < v) i++;
while (j >= l + 1 && arr[j] > v) j--;
if (i > j)
{
break;
}
swap(arr[i], arr[j]);
i++;
j--;
}
swap(arr[l], arr[j]);
return j;
}
template <typename T>
void __QuickSort2(T *arr,int l,int r)
{
if (l>=r)
{
return;
}
int p = __partition3(arr, l, r);
__QuickSort2(arr, l, p - 1);
__QuickSort2(arr, p + 1, r);
}
template <typename T>
void QuickSort2(T *arr, int n)
{
__QuickSort2(arr, 0,n-1);
}
#endif
随机快速排序 RadomQuickSort.h
#ifndef RADOMQUICKSORT_H
#define RADOMQUICKSORT_H
#include <iostream>
#include <stdlib.h>
using namespace std;
template <typename T>
int __Randpartition(T *arr, int l, int r)
{
//选择开头的数作为分割的数
int RAND = arr[rand() % (r - l + 1) + l];
swap(arr[l], RAND);
int i = arr[l];
//遍历数组,使得arr[l,l+1,...j]<arr[l],arr[j+1,...,k)>arr[l]
int j = l;
//如果当前数据大于arr[l],就无需改变位置,如果小于arr[l],就将当前数据与分割点的数据后一个数据交换
for (size_t k = j + 1; k <= r; k++)
{
if (arr[k]<i)
{
swap(arr[j + 1], arr[k]);
j++;
}
}
//最后一步,要记得将arr[l]和找到的分割点数据交换
swap(arr[l], arr[j]);
return j;
}
template <typename T>
void __RadomQuickSort(T *arr, int l, int r)
{
if (l >= r)
{
return;
}
int p = __Randpartition(arr, l, r);
__RadomQuickSort(arr, l, p - 1);
__RadomQuickSort(arr, p + 1, r);
}
template <typename T>
void RadomQuickSort(T *arr, int n)
{
__RadomQuickSort(arr, 0, n - 1);
}
#endif
快速排序 QuickSort.h
#ifndef QUICKSORT_H
#define QUICKSORT_H
using namespace std;
template <typename T>
int __partition(T *arr, int l, int r)
{
//选择开头的数作为分割的数
int i = arr[l];
//遍历数组,使得arr[l,l+1,...j]<arr[l],arr[j+1,...,k)>arr[l]
int j = l;
//如果当前数据大于arr[l],就无需改变位置,如果小于arr[l],就将当前数据与分割点的数据后一个数据交换
for (size_t k = j + 1; k <= r; k++)
{
if (arr[k]<i)
{
swap(arr[j + 1], arr[k]);
j++;
}
}
//最后一步,要记得将arr[l]和找到的分割点数据交换
swap(arr[l], arr[j]);
return j;
}
template <typename T>
void __QuickSort(T *arr, int l, int r)
{
if (l >= r)
{
return;
}
int p = __partition(arr, l, r);
__QuickSort(arr, l, p - 1);
__QuickSort(arr, p + 1, r);
}
template <typename T>
void QuickSort(T *arr, int n)
{
__QuickSort(arr, 0, n - 1);
}
#endif
SortTestHelper 函数
#ifndef SORTTESTHELPER_H
#define SORTTESTHELPER_H
#include <iostream>
#include <cassert>
#include <ctime>
#include <string>
using namespace std;
namespace SortTestHelper
{
//产生一个从[rangeL,rangeH]的随机数组,数组个数是n
int* generateRadomArray(int n,int rangeL,int rangeH)
{
//为了算法的健壮性,需要判断错误输入
assert(rangeL < rangeH);
int* arr = new int[n];
//时间为种子的随机数
srand((unsigned)time(NULL));
for (int i = 0;i < n;i++)
{
//生成rangeL到rangeH之间的随机数的算法
arr[i] = rand() % (rangeH - rangeL + 1) + rangeL;
}
return arr;
}
//产生近乎有序的随机数
int *generateNearlyOrderedArray(int n, int swapnum)
{
int *arr = new int[n];
srand((unsigned)time(NULL));
for (size_t i = 0; i < n; i++)
{
arr[i] = i;
}
for (size_t i = 0; i < swapnum; i++)
{
int x = rand() % n;
int y = rand() % n;
swap(arr[x], arr[y]);
}
return arr;
}
//打印数组:输入数组,数组元素的个数
template<typename T>
void printArr(T *arr,int n)
{
for (size_t i = 0; i < n; i++)
{
std::cout << arr[i] << " ";
}
std::cout << std::endl;
}
//判断是否已经排序
template<typename T>
bool ifSort(T *arr,int n)
{
for (size_t i = 0; i < n-1; i++)
{
if (arr[i]>arr[i+1])
{
return false;
}
}
return true;
}
//计算程序运行时间
template<typename T>
//函数输入参数是:所需要计算的运行的函数的名称,函数的指针,函数的输入数组,输入数组的个数
void sortTime(string funName,void(*sort)(T*arr, int), T* arr,int n)
{
clock_t startime = clock();
sort(arr,n);
clock_t endtime = clock();
assert(ifSort(arr, n));
std::cout <<funName<<"的运行时间:" << double(endtime-startime) / CLOCKS_PER_SEC <<"s"<< std::endl;
}
//拷贝随机生成的数组:输入要拷贝的数组指针(整型),输入需要拷贝多少个数
int* copyarr(int* a, int n)
{
int *arr = new int[n];
copy(a,a+n, arr);
return arr;
}
}
#endif
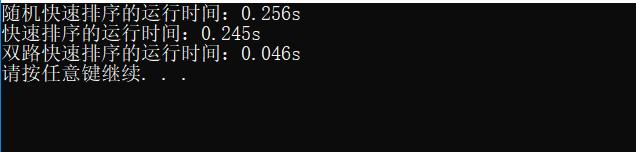
最终结果三种算法对10万个具有重复的数据的排序时间如下: